MANA for MPI: MPI-Agnostic Network-Agnostic Transparent Checkpointing¶

MANA is an MPI-Agnostic Network-Agnostic transparent checkpointing tool. MANA employs a novel split-process approach, in which a single system process contains two programs in its memory address space, the lower half, containing an MPI proxy application with MPI library, libc and other system libraries, and the upper half, containing the original MPI application and data (see the figure below). MANA tracks which memory regions belong to the upper and lower halves, and achieves MPI agnosticism by checkpointing only the upper-half memory and discarding the lower-half memory at checkpoint, and then reinitializing MPI library upon restart. MANA achieves network agnosticism by draining MPI messages before checkpointing. To make sure no checkpointing occurs when some ranks participate in a collective call, MANA prefaces all collective MPI calls with a trivial barrier. The real collective call happens only when all the ranks arrive or exit the trivial barrier. During the real collective calls the checkpointing is disabled, assuring that no messages floating in the network when checkpointing is initiated.

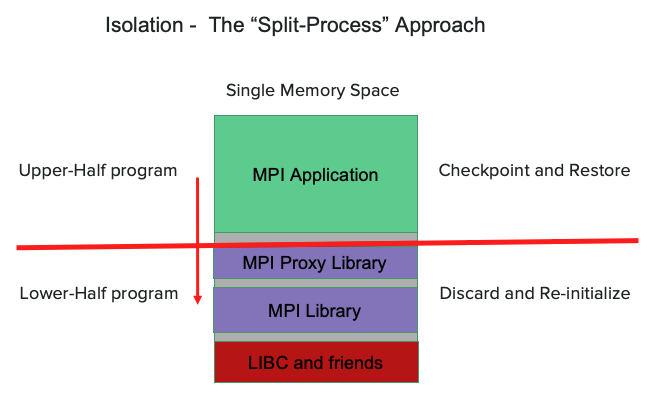
MANA addresses the critical maintenance cost of C/R tools over many combinations of MPI implementations and networks, and is transparent to the underlying MPI, network, libc library and Linux kernel. MANA is implemented as a plugin for DMTCP, therefore it lives completely in user space, and has been proven to be scalable to a large number of processes.

Starting from a proof-of-concept research code, MANA is under active development to use with production workloads. Its use on Perlmutter is therefore experimental. MANA may incur a high runtime overhead for applications that use MPI collective calls frequently. Developers have made significant progress on reducing the runtime overhead, and expect to fix the problem soon. Please report any issues you encounter at NERSC's Help Desk.

MANA on Perlmutter¶

To access, run

module load mana 

To see what the mana module does, run

module show mana 

Benefits of Checkpointing/Restart¶

You are encouraged to experiment with MANA with your applications, enabling checkpoint/restart in your production workloads. Benefits of checkpointing and restarting jobs with MANA includes,

• increased job throughput
• the capability of running jobs of any length
• a charging discount when using the preempt QOS
• reduced machine time loss due to system failures

Compile to Use MANA¶

To use MANA to checkpoint/restart your applications, you do not need to modify any of your codes. However, you must link your application dynamically, and build shared libraries for the libraries that your application depends on.

module unload darshan xalt
ftn -qopenmp -o jacobi.x jacobi.f90

Note that the darshan and xalt modules (a light-weight I/O profiling tool and a library tracking tool, respectively) are unloaded to avoid any complications they may add to MANA.

C/R MPI Applications with MANA¶

C/R Interactive Jobs¶

You can use MANA to checkpoint and restart your MPI application interactively, which is convenient when testing and debugging MANA jobs. Here are the steps on Perlmutter:

Checkpointing¶

1. Get on a compute node using the salloc command, e.g., requesting 1 CPU node for one hour

   salloc –N 1 –C cpu –t 1:00:00 -q interactive
   

   then load the mana module once on the compute node.

   module load mana 
   

2. Start the coordinator and specify the checkpoint interval, e.g., 300 seconds (-i300).

   mana_coordinator -i300
   

3. Then launch your application (a.out) with the mana_launch command.

   srun -n 64 -c 4 --cpu-bind=cores mana_launch ./a.out [arg1 ...]
   

   Then MANA will checkpoint your application every 300 seconds. You can terminate your running job once checkpoint files are generated.

Restarting¶

To restart your job from the checkpoint files, repeat steps 1-3 above, but replace the mana_launch command in step 3 with the mana_restart command. The mana_restart command line is as follows:

srun -n 64 -c 4 --cpu-bind=cores mana_restart 

Then MANA will restart from the checkpoint files and continue to run your application, checkpointing once every 300 seconds.

Note that MANA is implemented as a plugin in DMTCP, thereby uses the dmtcp_coordinator, dmtcp_launch, dmtcp_restart, and dmtcp_command commands of DMTCP as described in the DMTCP page, but with additional command line options. Since some of the command lines can be long, MANA provides bash scripts, mana_coordinator, mana_launch, mana_restart, and mana_status, respectively, to make the command lines short (easy to use).

In the example above, the mana_coordinator is a bash script that invokes the dmtcp_coordinator command as a daemon (--daemon) in the background. The full dmtcp_coordinator command line used in the above example is as follows:

dmtcp_coordinator --mpi --daemon --exit-on-last -q -i300 

Where the --mpi option is required to use MANA. The mana_launch and mana_restart are bash scripts that invoke the dmtcp_launch and dmtcp_restart, respectively, with added options for MANA. Here are the dmtcp_launch and dmtcp_restart command lines used in this example:

srun -n64 -c4 --cpu-bind=cores dmtcp_launch -h `hostname` --no-gzip --join --disable-dl-plugin --with-plugin $MANA_ROOT/lib/dmtcp/libmana.so ./a.out [arg1 ...]

srun -n64 -c4 --cpu-bind=cores dmtcp_restart --mpi -j  -h `hostname` --restartdir ./ 

MANA provides a command, mana_status, a bash script that invokes the dmtcp_command, to send the commands to the coordinator remotely, provided you need to get on the compute node where your job is running first.

mana_status --checkpoint  # checkpoint all processes 
mana_status --status      # query the status 
mana_status --quit        # kill all processes and quit               

All mana_* commands support command line options (use --help to see the list). For instance, you can save checkpoint files in a separate directory using the --ckptdir <directory name> option when invoking the mana_launch command. At restart, you can use the --restartdir <directory name> option to specify the checkpoint files for the mana_restart command.

C/R Batch Jobs¶

Assume the job you wish to checkpoint is run.slurm as shown below, in which you request Perlmutter CPU nodes to run an MPI application for 24 hours. You can checkpoint and restart this job using the C/R job scripts below, run_launch.slurm and run_restart.slurm.

Perlmutter CPU¶

#!/bin/bash 
#SBATCH -J test
#SBATCH -q regular
#SBATCH -N 2 
#SBATCH -C cpu
#SBATCH -t 24:00:00
#SBATCH -o %x-%j.out
#SBATCH -e %x-%j.err

srun -n 64 ./a.out

#!/bin/bash
#SBATCH -J test_cr
#SBATCH -q preempt
#SBATCH -N 2 
#SBATCH -C cpu
#SBATCH -t 24:00:00
#SBATCH -o %x-%j.out
#SBATCH -e %x-%j.err

#c/r with mana 
module load mana 

#checkpointing once every hour
mana_coordinator -i 3600

#running under mana control
srun -n 64 mana_launch ./a.out

#!/bin/bash
#SBATCH -J test_cr
#SBATCH -q preempt
#SBATCH -N 2 
#SBATCH -C cpu
#SBATCH -t 24:00:00
#SBATCH -o %x-%j.out
#SBATCH -e %x-%j.err

#c/r with mana 
module load mana 

#checkpointing once every hour
mana_coordinator -i 3600

#restarting from checkpoint files
srun -n 64 mana_restart

To run the job, just submit the C/R job scripts above,

sbatch run_launch.slurm
sbatch run_restart.slurm   #if the first job is pre-terminated
sbatch run_restart.slurm   #if the second job is pre-terminated
...

The first job will run with a specified time limit of 24 hours. If it is preempted before then, you will need to submit the restart job, run_restart.slurm. You may need to submit it multiple times until the job completes or has run for 24 hours as requested. You can use the job dependencies to submit all your C/R jobs at once (you may need to submit many more restart jobs than actually needed). You can also combine the two C/R job scripts into one (see the next section), and then submit it multiple times as dependent jobs all at once. However, this is still not as convenient as submitting the job script run.slurm only once. The good news is that you can automate the C/R jobs using the features supported in Slurm and a trap function (see the next section). The job scripts in the next section are recommended to run C/R jobs.

Automate C/R Jobs¶

C/R job submissions can be automated using preemptible jobs, so that you just need to submit a single job script once as you would with your original job script, run.slurm.

Here is the sample job script:

Perlmutter CPU¶

#!/bin/bash 
#SBATCH -J test
#SBATCH -q preempt 
#SBATCH -N 2             
#SBATCH -C cpu
#SBATCH -t 24:00:00 
#SBATCH -e %x-%j.err 
#SBATCH -o %x-%j.out
#
#SBATCH --comment=48:00:00
#SBATCH --signal=B:USR1@300
#SBATCH --requeue
#SBATCH --open-mode=append

module load mana nersc_cr

#checkpointing once every hour
mana_coordinator -i 3600

#checkpointing/restarting jobs
if [[ $(restart_count) == 0 ]]; then

    srun -n 64 mana_launch ./a.out &
elif [[ $(restart_count) > 0 ]] && [[ -e dmtcp_restart_script.sh ]]; then

    srun -n 64 mana_restart &
else

    echo "Failed to restart the job, exit"; exit
fi

# requeueing the job if remaining time >0
ckpt_command=ckpt_mana    #checkpointing additionally right before the job hits the walllimit 
requeue_job func_trap USR1

wait

This job script combines the two C/R job scripts in the previous section, run_launch.slurm and run_restart.slurm by checking the restart count of the job (if block). Each job will run with a time anywhere between the 2 hours guaranteed by the preempt QOS and time limit (-t), checkpointing once every hour (-i 3600). In the C/R job scripts, in addition to loading the mana module, the nersc_cr module is loaded as well, which provides a set of bash functions to manage C/R jobs, e.g., restart_count, requeue_job, func_trap, ckpt_mana, etc., that are used in the job script.

What's new in this script is that

1. It can automatically track the remaining walltime, and resubmit itself until the job completes or the accumulated run time reaches the desired walltime (48 hours in this example).

2. Optionally, each job checkpoints one more time 300 seconds before the job hits the allocated time limit.

3. There is only one job ID, and one standard output/error file associated with multiple shorter jobs.

These features are enabled with the following additional sbatch flags and a bash function requeue_job, which traps the signal (USR1) sent from the batch system:

#SBATCH --comment=48:00:00         #comment for the job
#SBATCH --signal=B:USR1@<sig_time> 
#SBATCH --requeue                  #specify job is requeueable
#SBATCH --open-mode=append         #to append standard out/err of the requeued job  
                                   #to that of the previously terminated job

#requeueing the job if remaining time >0
ckpt_command=ckpt_mana 
requeue_job func_trap USR1

wait

where the --comment sbatch flag is used to specify the desired walltime and to track the remaining walltime for the job (after pre-termination). You can specify any length of time, e.g., a week or even longer. The --signal flag is used to request that the batch system sends user-defined signal USR1 to the batch shell (where the job is running) sig_time seconds (e.g., 300) before the job hits the wall limit. This time should match the checkpoint overhead of your job.

Upon receiving the signal USR1 from the batch system (300 seconds before the job hits the wall limit), the requeue_job executes the following commands (contained in a function func_trap provided on the reuque_job command line in the job script):

mana_status --checkpoint     #checkpoint the job if ckpt_command=ckpt_mana  
scontrol requeue $SLURM_JOB_ID #requeue the job 

If your job completes before the job hits the wall limit, then the batch system will not send the USR1 signal, and the two commands above will not be executed (no additional checkpointing and no more requeued job). The job will exit normally.

For more details about the requeue_job and other functions used in the C/R job scripts, refer to the script cr_functions.sh provided by the nersc_cr module. (type module show nersc_cr to see where the script resides). You may consider making a local copy of this script, and modifying it for your use case.

To run the job, simply submit the job script,

sbatch run_cr.slurm

C/R Serial/Threaded Applications¶

If you run serial/threaded applications, we recommend that you use DMTCP to checkpoint and restart your jobs. See the DMTCP page for detailed instructions. MANA is recommended for checkpointing MPI applications.

Resources¶

• DMTCP website

• MANA for MPI: MPI-Agnostic Network-Agnostic Transparent Checkpointing

• MANA GitHub

• User training on Checkpoint/Restart (May 2021):

  • Checkpoint/Restart MPI Applications with MANA on Cori (Slides) (Recording)

  • Checkpoint/Restart VASP Jobs Using MANA on Cori (Slides)